Gremlin is the graph traversal language of Apache TinkerPop. Gremlin is a functional, data-flow language that enables users to succinctly express complex traversals on (or queries of) their application's property graph. Every Gremlin traversal is composed of a sequence of (potentially nested) steps. A step performs an atomic operation on the data stream. Every step is either a map-step (transforming the objects in the stream), a filter-step (removing objects from the stream), or a sideEffect-step (computing statistics about the stream). The Gremlin step library extends on these 3-fundamental operations to provide users a rich collection of steps that they can compose in order to ask any conceivable question they may have of their data for Gremlin is Turing Complete.

Explaining Gremlin

There are different levels on which gremlin can be explained:

On this page the goal is to cover all 4 levels with a focus on Java being applied to the modern example. The source code TestSteps.java is available on github.

Graph

A Graph G= (V, E) consist of a finite set of vertices V and a finite set of edges E ⊆ V×V.

An Element of a Graph is either a vertice or an edge.

A Propertygraph allows all elements (vertice or edge) of a graph to have properties. Each property is a name/value pair.

The Modern example

The "modern" graph is shipped with gremlin as a standard example.

The graph has 6 edges and 6 vertices.

It consists of :

vertice person (name: marko, age:29)
vertice person (name: vadas, age:27)
vertice software (name: lop, lang: java)
vertice person (name: josh, age:32)
vertice software (name: ripple, lang: java)
vertice person (name: peter, age:35)
edge knows 1->2 (weight: 0.5)
edge knows 1->4 (weight: 1.0)
edge created 1->3 (weight: 0.4)
edge created 4->5 (weight: 1.0)
edge created 4->3 (weight: 0.4)
edge created 6->3 (weight: 0.2)

In Gremlin edges and vertices have a set of properties. Each property is a name/value pair. One important property is the id of a vertice or edge. E.g. the vertice for peter has the id 6 and a property with the name "age" and the value 35 and another property with the name "name" and the value "peter".

GraphTraversal

One of the core concepts of tinkerpop/gremlin is the GraphTraversal It's interface has a generic definition as:

public interface GraphTraversal<S,E> extends Traversal<S,E>

and at https://markorodriguez.com/ the Author Marko Rodriguez explains the ideas behind using an generic approach vor handling Graphs. The Java implementation is available on github.

S is a generic Start class, and E is a generic End class as explained in the Apache Tinkerpop documentation.

GraphTraversalSource

A Graph Traversal Source is the starting point for working with a graph. The convention is to name this starting point

or

g()

In our tests we'll use a GraphTraversalSource for the modern example

  /**
   * common access to GraphTraversalSource
   * @return - the graph traversal
   */
  public GraphTraversalSource g() {
    Graph graph = TinkerFactory.createModern();
    GraphTraversalSource g = graph.traversal();
    return g;
  }

JUnit Testcase

  @Test
  public void testTraversal() {
    assertEquals(6,g().E().count().next().longValue());
    assertEquals(6,g().V().count().next().longValue());
  }

E() gives you access to the edges of a graph traversal. V() gives you access to the vertices of a graph traversal. In the above example we simply count the edges and vertices and check our assumption that there are 6 edges and 6 vertices in the modern example graph.

Steps

As explained in Gremlin_Basics: "The Gremlin graph traversal language defines approximately 30 steps which can be understood as the instruction set of the Gremlin traversal machine.

A regular computer has a CPU with an Instruction Pointer which tells the machine to take the instruction at that memory address and execute it next. There are also instruction that can manipulate the instruction pointer with the effect of the return from a function or a goto to a different part of the program.

Gremlin instead works on a sequence of steps and each step the "graph traversal machine" will take it's current state and execute the step to reach a new state of affairs.

The gremlin steps are useful in practice, with typically only 10 or so of them being applied in the majority of cases. Each of the provided steps can be understood as being a specification of one of the 5 general types enumerated below".

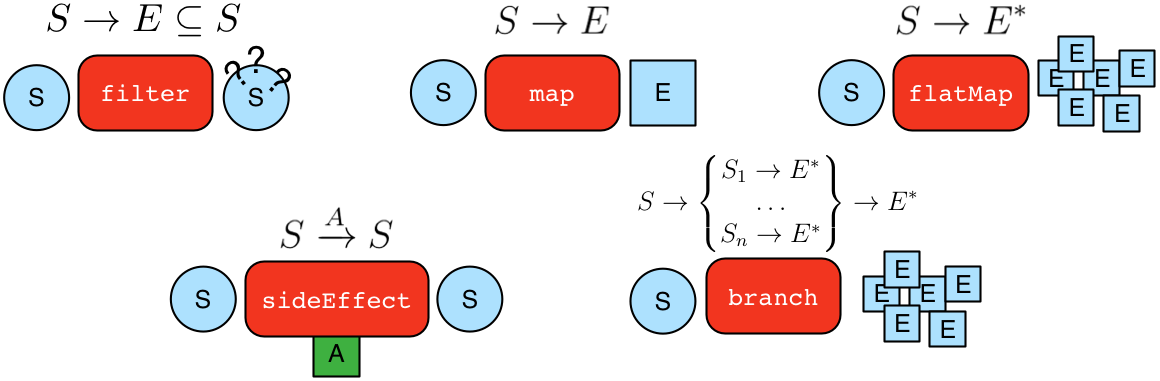
Alphabetical table of Steps

There are 58 Steps described on this page

name	kind	reference	text
addE	sideEffect	addedge-step	is used to add edges to the graph
addV	sideEffect	addvertex-step	is used to add vertices to the graph
aggregate	sideEffect	aggregate-step	is used to aggregate all the objects at a particular point of traversal into a Collection
and	filter	and-step	ensures that all provided traversals yield a result
as	modulator	as-step	is not a real step, but a "step modulator" similar to by() and option(). With as(), it is possible to provide a label to the step that can later be accessed by steps and data structures that make use of such labels — e.g., select(), match(), and path
both	flatMap		maps the current elements to the vertices at the boths ends of the edges.
bothE	flatMap		maps the current elements to both the in and outgoing edges.
bothV	flatMap		maps the current edges to both the ingoing and outgoing Vertices.
branch	general	general-steps	Splits the traverser
by	modulator	by-step	is not an actual step, but instead is a "step-modulator" similar to as() and option(). If a step is able to accept traversals, functions, comparators, etc. then by() is the means by which they are added. The general pattern is step().by()…by(). Some steps can only accept one by() while others can take an arbitrary amount.
cap	barrier	cap-step	Iterates the traversal up to the itself and emits the side-effect referenced by the key. If multiple keys are supplied then the side-effects are emitted as a Map.
choose	branch	choose-step	routes the current traverser to a particular traversal branch option. With choose(), it is possible to implement if/then/else-semantics as well as more complicated selections.
coalesce	flatMap	coalesce-step	The coalesce()-step evaluates the provided traversals in order and returns the first traversal that emits at least one element.
coin	filter	coin-step	randomly filters out traversers with the given probability
count	reducing barrier	count-step	counts the total number of represented traversers in the streams (i.e. the bulk count).
emit	modulator	emit-step	is not an actual step, but is instead a step modulator for repeat() (find more documentation on the emit() there).
explain	terminal	terminal-steps	will return a TraversalExplanation. A traversal explanation details how the traversal (prior to explain()) will be compiled given the registered traversal strategies. A TraversalExplanation has a toString() representation with 3-columns. The first column is the traversal strategy being applied. The second column is the traversal strategy category: [D]ecoration, [O]ptimization, [P]rovider optimization, [F]inalization, and [V]erification. Finally, the third column is the state of the traversal post strategy application. The final traversal is the resultant execution plan.
fill	terminal	terminal-steps	fill(collection) will put all results in the provided collection and return the collection when complete.
filter	general	general-steps	Continues processing based on the given filter condition.
flatMap	general	general-steps	transforms the current step in a one to many fashion.
fold	reducing barrier	fold-step	There are situations when the traversal stream needs a "barrier" to aggregate all the objects and emit a computation that is a function of the aggregate. The fold()-step (map) is one particular instance of this. Please see unfold()-step for the inverse functionality.
has	filter	has-step	filters vertices, edges, and vertex properties based on their properties. This step has quite a few variations.
hasNext	terminal	terminal-steps	determines whether there are available results
id	map	id-step	maps the traversal to the ids of the current elements.
in	flatMap		maps the current elements to the vertices at the end of the ingoing edges.
inE	flatMap		maps the current elements to the the ingoing edges.
inV	flatMap		maps the current edges to the the ingoing Vertices.
is	filter	is-step	filters elements that fullfill the given predicate. Variant: Filters elements that are equal to the given Object.
iterate	terminal	terminal-steps	Iterates the traversal presumably for the generation of side-effects. See https://stackoverflow.com/questions/47403296/iterate-step-is-used-in-the-end-of-the-command-when-creating-nodes-and-edges-t
label	map	label-step	maps the traversal to the labels of the current elements.
limit	filter	limit-step
map	general	general-steps	transforms the current step element to a new element (which may be empty). see also https://stackoverflow.com/questions/51015636/in-gremlin-how-does-map-really-work
match	map	match-step	see https://stackoverflow.com/questions/55609832/is-threre-a-document-about-how-gremlin-match-works
max	reducing barrier	max-step	operates on a stream of comparable objects and determines which is the last object according to its natural order in the stream.
mean	reducing barrier	mean-step	operates on a stream of numbers and determines the average of those numbers.
min	reducing barrier	min-step	operates on a stream of comparable objects and determines which is the first object according to its natural order in the stream.
next	terminal	terminal-steps	will return the next result.next(n) will return the next n results in a list
option	modulator	option-step	An option to a branch() or choose()
or	filter	or-step	ensures that at least one of the provided traversals yield a result.
order	map	order-step	orders the traversal elements
out	flatMap		maps the current elements to the vertices at the end of the outgoing edges.
outE	flatMap		maps the current elements to the the outgoing edges.
outV	flatMap		The outV step maps the current edges to the outgoing Vertices.
path	map	path-step
promise	terminal	terminal-steps	can only be used with remote traversals to Gremlin Server or RGPs. It starts a promise to execute a function on the current Traversal that will be completed in the future.
property	sideEffect	addproperty-step	is used to add properties to the elements of the graph
range	filter	range-step
repeat	branch	repeat-step	is used for looping over a traversal given some break predicate
select	map	select-step
sideEffect	general	general-steps	performs some operation on the traverser and passes it to the next step.
... further results

Stephierarchy

All steps are based on five general steps. Click on any of the steps below to see the explanation for the step

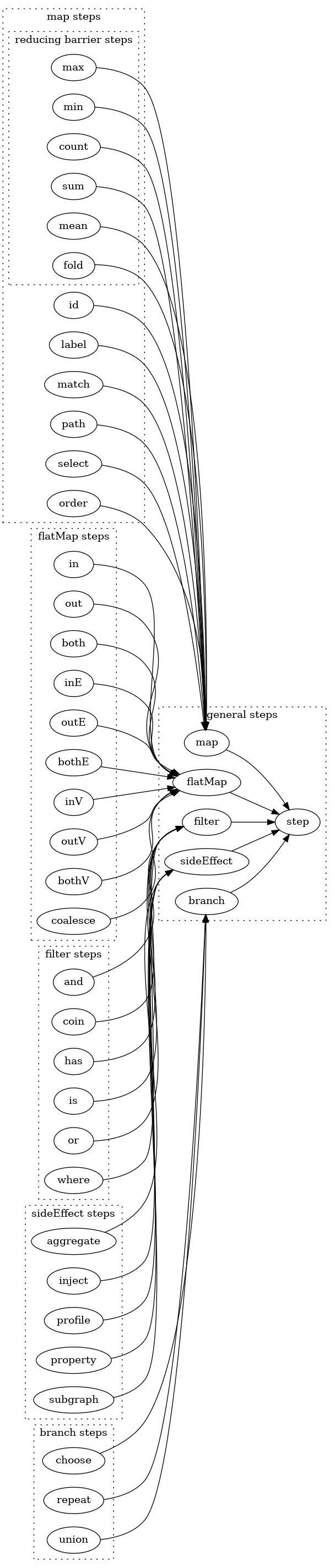
terminal Steps

hasNext Step

The hasNext step determines whether there are available results

  @Test
  public void testHasNext() {
    assertTrue(g().V(1).hasNext());
    assertFalse(g().V(7).hasNext());
  }

next Step

The next step will return the next result.next(n) will return the next n results in a list

. @Test
  public void testNext() {
    assertEquals("v[1]",g().V().next().toString());
    assertEquals("v[1]",g().V(1).next().toString());
    assertEquals("[v[1], v[2]]",g().V(1,2,3).next(2).toString());
  }

tryNext Step

The tryNext step will return an Optional and thus, is a composite of hasNext()/next()

  @Test
  public void testTryNext() {
    assertTrue(g().V(1).tryNext().isPresent());
    assertFalse(g().V(7).tryNext().isPresent());
  }

toList Step

The toList step will return all results in a list

  @Test
  public void testToList() {
    List<Vertex> vlist = g().V().toList();
    assertEquals("[v[1], v[2], v[3], v[4], v[5], v[6]]", vlist.toString());
    List<Edge> elist = g().E(7,8,9).toList();
    assertEquals(
        "[e[7][1-knows->2], e[8][1-knows->4], e[9][1-created->3]]",
        elist.toString());
  }

toSet Step

The toSet step will return all results in a set and thus, duplicates removed

  @Test
  public void testToSet() {
    Set<Vertex> vset = g().V(1,2,2,3,4).toSet();
    assertEquals("[v[1], v[2], v[3], v[4]]", vset.toString());
    Set<Edge> set = g().E(7,8,9,7,8,9).toSet();
    assertEquals(
        "[e[7][1-knows->2], e[8][1-knows->4], e[9][1-created->3]]",
        set.toString());
  }

toBulkSet Step

The toBulkSet step will return all results in a weighted set and thus, duplicates preserved via weighting

  @Test
  public void testToBulkSet() {
    BulkSet<Vertex> vset = g().V(1,2,2,3,4).toBulkSet();
    assertEquals(2,vset.asBulk().get(g().V(2).next()).longValue());
  }

fill Step

The fill step fill(collection) will put all results in the provided collection and return the collection when complete.

  @Test
  public void testFill() {
    List<Vertex> vlist=new LinkedList<Vertex>();
    List<Vertex> rvlist = g().V().fill(vlist);
    assertEquals(vlist,rvlist);
    assertEquals("[v[1], v[2], v[3], v[4], v[5], v[6]]", vlist.toString());
  }

map Steps

id Step

The id step maps the traversal to the ids of the current elements.

  @Test
  public void testId() {
    List<Object> vids = g().V().id().toList();
    assertEquals(6,vids.size());
    assertEquals("[1, 2, 3, 4, 5, 6]",vids.toString());
    List<Object> eids = g().E().id().toList();
    assertEquals(6,eids.size());
    assertEquals("[7, 8, 9, 10, 11, 12]",eids.toString());
  }

label Step

The label step maps the traversal to the labels of the current elements.

  @Test
  public void testLabel() {
    List<String> vlabels = g().V().label().toList();
    assertEquals(6,vlabels.size());
    assertEquals("[person, person, software, person, software, person]",vlabels.toString());
    List<String> elabels = g().E().label().toList();
    assertEquals(6,elabels.size());
    assertEquals("[knows, knows, created, created, created, created]",elabels.toString());
  }

match Step

The match step see https://stackoverflow.com/questions/55609832/is-threre-a-document-about-how-gremlin-match-works

path Step

The path step

select Step

The select step

order Step

The order step

reducing barrier Steps

count Step

The count step counts the total number of represented traversers in the streams (i.e. the bulk count).

@Test
  public void testCount() {
    assertEquals(6,g().V().count().next().longValue());
    assertEquals(4,g().V().hasLabel("person").count().next().intValue());
    assertEquals(2,g().V().hasLabel("software").count().next().intValue());
    assertEquals(4,g().E().hasLabel("created").count().next().intValue());
    assertEquals(2,g().E().hasLabel("knows").count().next().intValue());
  }

min Step

The min step operates on a stream of comparable objects and determines which is the first object according to its natural order in the stream.

@Test
  public void testMin() {
    assertEquals(27,g().V().values("age").min().next());
    assertEquals(0.2,g().E().values("weight").min().next());
    assertEquals("josh",g().V().values("name").min().next());
  }

max Step

The max step operates on a stream of comparable objects and determines which is the last object according to its natural order in the stream.

@Test
  public void testMax() {
    assertEquals(35,g().V().values("age").max().next());
    assertEquals(1.0,g().E().values("weight").max().next());
    assertEquals("vadas",g().V().values("name").max().next());
  }

mean Step

The mean step operates on a stream of numbers and determines the average of those numbers.

@Test
  public void testMean() {
    assertEquals(30.75, g().V().values("age").mean().next());
    assertEquals(0.583, g().E().values("weight").mean().next().doubleValue(),
        0.001);
    try {
      assertEquals("josh", g().V().values("name").mean().next());
    } catch (Exception e) {
      assertEquals("java.lang.String cannot be cast to java.lang.Number",e.getMessage());
    }
  }

sum Step

The sum step operates on a stream of numbers and sums the numbers together to yield a result

@Test
  public void testSum() {
    assertEquals(123, g().V().values("age").sum().next().intValue());
    assertEquals(3.5, g().E().values("weight").sum().next().doubleValue(),0.01);
  }

fold Step

The fold step There are situations when the traversal stream needs a "barrier" to aggregate all the objects and emit a computation that is a function of the aggregate. The fold()-step (map) is one particular instance of this. Please see unfold()-step for the inverse functionality.

@Test
  public void testFold() {
    List<Object> knowsList1 = g().V(1).out("knows").values("name").fold().next();
    assertEquals("[vadas, josh]",knowsList1.toString());
  }

flatMap Steps

in Step

The in step maps the current elements to the vertices at the end of the ingoing edges.

  @Test
  public void testIn() {
    assertEquals("[v[1], v[1], v[4], v[6], v[1], v[4]]",
        g().V().in().toList().toString());
    assertEquals("[v[1], v[4], v[6], v[4]]",
        g().V().in("created").toList().toString());
    assertEquals("[v[1], v[1]]", g().V().in("knows").toList().toString());
    assertEquals("[v[1], v[1], v[4], v[6], v[1], v[4]]",
        g().V().in("created","knows").toList().toString());
  }

out Step

The out step maps the current elements to the vertices at the end of the outgoing edges.

  @Test
  public void testOut() {
    assertEquals("[v[3], v[2], v[4], v[5], v[3], v[3]]",
        g().V().out().toList().toString());
    assertEquals("[v[3], v[5], v[3], v[3]]",
        g().V().out("created").toList().toString());
    assertEquals("[v[2], v[4]]", g().V().out("knows").toList().toString());
    assertEquals("[v[3], v[2], v[4], v[5], v[3], v[3]]",
        g().V().out("created","knows").toList().toString());
  }

both Step

The both step maps the current elements to the vertices at the boths ends of the edges.

  @Test
  public void testBoth() {
    assertEquals("[v[5], v[3], v[1]]",
      g().V(4).both().toList().toString());
    assertEquals("[v[5], v[3]]",
        g().V(4).both("created").toList().toString());
    assertEquals("[v[1]]", g().V(4).both("knows").toList().toString());
    assertEquals("[v[5], v[3], v[1]]",
        g().V(4).both("created","knows").toList().toString());
  }

inE Step

The inE step maps the current elements to the the ingoing edges.

@Test
  public void testInE() {
    assertEquals(
        "[e[7][1-knows->2], e[9][1-created->3], e[11][4-created->3], e[12][6-created->3], e[8][1-knows->4], e[10][4-created->5]]",
        g().V().inE().toList().toString());
    assertEquals(
        "[e[9][1-created->3], e[11][4-created->3], e[12][6-created->3], e[10][4-created->5]]",
        g().V().inE("created").toList().toString());
    assertEquals("[e[7][1-knows->2], e[8][1-knows->4]]",
        g().V().inE("knows").toList().toString());
    assertEquals(
        "[e[7][1-knows->2], e[9][1-created->3], e[11][4-created->3], e[12][6-created->3], e[8][1-knows->4], e[10][4-created->5]]",
        g().V().inE("created", "knows").toList().toString());
  }

outE Step

The outE step maps the current elements to the the outgoing edges.

  @Test
  public void testOutE() {
    assertEquals(
        "[e[9][1-created->3], e[7][1-knows->2], e[8][1-knows->4]]",
        g().V(1).outE().toList().toString());
    assertEquals(
        "[e[9][1-created->3]]",
        g().V(1).outE("created").toList().toString());
    assertEquals("[e[7][1-knows->2], e[8][1-knows->4]]",
        g().V(1).outE("knows").toList().toString());
    assertEquals(
        "[e[9][1-created->3], e[7][1-knows->2], e[8][1-knows->4]]",
        g().V(1).outE("created", "knows").toList().toString());
  }

bothE Step

The bothE step maps the current elements to both the in and outgoing edges.

  @Test
  public void testBothE() {
    assertEquals("[e[10][4-created->5], e[11][4-created->3], e[8][1-knows->4]]",
        g().V(4).bothE().toList().toString());
    assertEquals("[e[10][4-created->5], e[11][4-created->3]]",
        g().V(4).bothE("created").toList().toString());
    assertEquals("[e[8][1-knows->4]]",
        g().V(4).bothE("knows").toList().toString());
    assertEquals("[e[10][4-created->5], e[11][4-created->3], e[8][1-knows->4]]",
        g().V(4).bothE("created", "knows").toList().toString());
  }

inV Step

The inV step maps the current edges to the the ingoing Vertices.

  @Test
  public void testInV() {
    assertEquals("[v[2], v[4], v[3], v[5], v[3], v[3]]",
        g().E().inV().toList().toString());
    assertEquals("[v[3]]", g().E(9).inV().toList().toString());
  }

outV Step

The outV step The outV step maps the current edges to the outgoing Vertices.

  @Test
  public void testOutV() {
    assertEquals("[v[1], v[1], v[1], v[4], v[4], v[6]]",
        g().E().outV().toList().toString());
    assertEquals("[v[1]]", g().E(9).outV().toList().toString());
  }

bothV Step

The bothV step maps the current edges to both the ingoing and outgoing Vertices.

  @Test
  public void testBothV() {
    assertEquals("[v[4], v[3]]",
        g().E(11).bothV().toList().toString());
    assertEquals("[v[1], v[3]]", g().E(9).bothV().toList().toString());
  }

coalesce Step

The coalesce step The coalesce()-step evaluates the provided traversals in order and returns the first traversal that emits at least one element.

General Steps

filter Step

Continues processing based on the given filter condition.

  @Test
  public void testFilter() {
    assertEquals(3,g().V().filter(out()).count().next().longValue());
    assertEquals(4,g().V().filter(in()).count().next().longValue());
    assertEquals(5,g().E().filter(values("weight").
      is(P.gte(0.4))).count().next().longValue());
  }

There are 3 vertices having outgoing edges and 4 vertices having incoming edges in the modern example graph. There are 4 edges having a weight>=0.4;

map Step

A map step transforms the current step element to a new element (which may be empty). see also https://stackoverflow.com/questions/51015636/in-gremlin-how-does-map-really-work

 @Test
  public void testMap() {
    assertEquals(6,g().V().map(values("name")).count().next().longValue());
    assertEquals(4,g().V().map(hasLabel("person")).count().next().longValue());
    assertEquals(2,g().V().map(has("lang","java")).count().next().longValue());
    List<Edge> outEdges = g().V().map(outE()).toList();
    assertEquals(3,outEdges.size());
    List<Object> edges = g().E().map(has("weight",0.4)).toList();
    assertEquals(2,edges.size());
    for (Object edge:edges) {
      assertTrue(edge instanceof Edge);
    }
  }

There are 6 vertices having a name property. There are 4 vertices with a "person" label. There are 2 vertices with the lang property having the value "java".There are 3 vertices having out edges. The toList() call returns a list of Edges. There are 2 edges having a weight of 0.4. The map step toList() returns a list of the edges for this last example (which are returned as generic objects).

flatMap Step

A flatMap step transforms the current step in a one to many fashion.

 @Test
  public void testflatMap() {
    assertEquals(6,g().V().flatMap(values("name")).count().next().longValue());
    assertEquals(4,g().V().flatMap(hasLabel("person")).count().next().longValue());
    assertEquals(2,g().V().flatMap(has("lang","java")).count().next().longValue());
    List<Edge> outEdges = g().V().flatMap(outE()).toList();
    assertEquals(6,outEdges.size());
    List<Object> edges = g().E().flatMap(has("weight",0.4)).toList();
    assertEquals(2,edges.size());
    for (Object edge:edges) {
      assertTrue(edge instanceof Edge);
    }
  }

Note the difference to the testMap step. Only the outE() parameter behaves different. In the map() case only the first Edge is considered - in the flatMap case all edges are considered.

sideEffect Step

A sideEffect steps performs some operation on the traverser and passes it to the next step.

  @Test
  public void testSideEffect() {
    assertEquals(6,g().V().sideEffect(addE("sideedge")).outE().
      hasLabel("sideedge").count().next().longValue());
  }

The sideffect in this example JUnit test case adds edges "on the fly".

branch Step

Split the traverser

  @Test
  public void testBranch() {
   
  }

What links here

Links

Stackoverflow Questions

Recipes

Cycle Detection

Practical Gremlin: An Apache TinkerPop Tutorial by Kelvin Lawrence

Traversing Graphs with Gremlin

Gremlin